Die Webseiten der Fachschaft Informatik am ERG Saalfeld

Das Rucksackproblem als Beispiel für "praktisch nicht berechenbar"

Die im Folgenden angegebene Darstellung des Rucksackproblems wurde von den Seiten von "inf-schule.de" übernommen und an das Layout dieser Seiten angepasst. Diese Seite steht deshalb wie die Seiten des Originals unter der Lizenz CC BY-SA 4.0.

Ein Rucksack voller Geschenke

Franziska ist die Gewinnerin bei der neuen Fernsehshow "Knapsack". Als Gewinn erhält sie einen Rucksack, in den sie weitere Gegenstände aus einer vorgegebenen Auswahl einpacken kann.

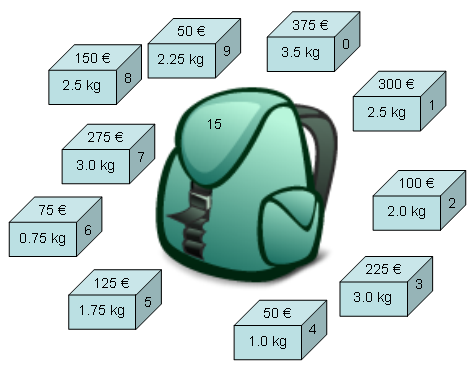
Es gibt allerdings einen kleinen Haken. Der Rucksack wird nach dem Einpacken der Gegenstände gewogen. Überschreitet das Gesamtgewicht die maximales Traglast von 15 kg, gibt es keinen Gewinn.

Das Rucksackproblem

Das Rucksackproblem lässt sich allgemein wie folgt formulieren:

Gegeben sind n Gegenstände mit ihren Gewichten und Werten. Gegeben ist zusätzlich ein Grenzgewicht, das die maximale Traglast des Rucksacks beschreibt. Gesucht ist eine Kombination von Gegenständen, so dass das Grenzgewicht nicht überschritten wird und der Gesamtwert der Gegenstände möglichst hoch ist.

Formal lässt das Rucksackproblem so formulieren:

Gegeben sind n Zahlenpaare (g₀, w₀), ..., (g_n-1, w_n-1) (die Gewicht und Wert von n Gegenständen beschreiben). Gegeben ist zusätzlich eine Grenzzahl G (die die maximale Traglast des Rucksacks beschreibt). Alle diese Zahlen sind beliebige (positive) Dezimalzahlen.

Gesucht ist eine 0-1-Folge x₀, ..., x_n-1 (die die Auswahl der Gegenstände beschreibt: 0 - nicht einpacken; 1 - einpacken),
so dass   x₀*g₀ + ... + x_n-1*g_n-1 <= G   gilt und   x₀*w₀ + ... + x_n-1*w_n-1   maximal ist.

Ein einfacher Lösungsalgorithmus

Kombinationen ausprobieren

Eine - zugegebenermaßen - wenig elegante Lösung des Rucksackproblems besteht darin, alle möglichen Kombinationen von Gegenständen zu betrachten und die zugehörigen Gesamtgewichte und Gesamtwerte zu berechnen und aus all den ermittelten Zahlenwerten die gesuchte Kombination zu bestimmen.

Ein Algorithmus zum Lösungsverfahren

Ein Algorithmus zur oben beschriebenen Idee lässt sich leicht formulieren, z.B. so:

  Übergabe:
  erzeuge eine erste kombination, z.B. '00000000'
  maxKombination = kombination
  maxWert = Gesamtwert von kombination
  SOLANGE noch nicht alle Kombinationen durchlaufen sind:
      erzeuge eine neue kombination
      WENN der Gesamtwert von kombination > maxWert und
           das Gesamtgewicht von kombination <= grenzgewichtRucksack:
          maxKombination = kombination
          maxWert = Gesamtwert von kombination
  Rückgabe: (maxKombination, maxWert, Gesamtgewicht von maxKombination)

Eine Implementierung zum Algorithmus

Zur Implementierung müssen u.a. alle möglichen Kombinationen erzeugt werden. Wir gehen dabei so vor:

Eine Kombination wird durch eine 0-1-Zeichenkette beschrieben, die für jeden Gegenstand festlegt, ob er eingepackt wird ('1') oder nicht ('0'). So beschreibt z.B. die Zeichenkette '0010000000' eine Situation, in der nur der Gegenstand mit der Nummer 2 ausgewählt wird (beachte: wie fangen bei 0 an zu zählen).

Bei n Gegenständen gibt es 2ⁿ mögliche Kombinationen bzw. 0-1-Zeichenketten. Wir erzeugen diese systematisch, indem wir die Zahlen 0..2ⁿ-1 durchlaufen und aus den Dualdarstellungen dieser Zahlen die 0-1-Bitmuster generieren.

Auf der als Quelle angegebenen Seite ist ein (noch zu ergänzendes) Demoprogramm in Python angegeben, dass alle möglichen Kombinationen sowie deren Gesamtwert und Gesamtgewicht bestimmt.

Komplexitätsbetrachtungen

Komplexität des Algorithmus

Eine naive Beschreibung der Komplexität des oben gezeigten Algorithmus geht von folgenden Annahmen aus:

Die Problemgröße wird durch die Anzahl n der Gegenstände festgelegt.

Als Kostenmaß wählen wir die Anzahl der zu untersuchenden Kombinationen. Es ergibt sich dann die Kostenfunktion K(n) = 2ⁿ.

Diese Kostenfunktion ist eine Exponentialfunktion. Der Algorithmus hat demnach eine exponentielle Komplexität.

Komplexität des Problems

Ob das Rucksackproblem selbst eine exponentielle Komplexität hat, ist hierdurch noch nicht erwiesen. Es könnte Algorithmen geben, die das Problem viel schneller - z.B. mit polynomialer Komplexität - lösen.

Tatsächlich gibt es einen Algorithmus, der das Rucksackproblem viel effizienter als der oben gezeigte Algorithmus bearbeiten. Er beruht auf der Idee, dass man das Problem, einen Rucksack bei n Gegenständen optimal zu packen, auf das Problem, einen Rucksack bei n-1 Gegenständen optimal zu packen, reduzieren kann.

Analysiert man die Komplexität dieses Algorithmen, so erweist sich die oben vorgenommene "naive" Problembeschreibung als inadäquat. Man muss die Größe und Verarbeitung der insgesamt 2n+1 zu verarbeitenden Ausgangszahlen differenzierter betrachten. Insbesondere muss man berücksichtigen, dass sinnvollerweise die Rucksackkapazität mit wachsender Anzahl von Gegenständen auch wachsen sollte. Es erweist sich dann, dass bei diesem Algorithmus trotz großer Verbesserungen dennoch eine exponentielle Komplexität vorliegt.

Alle bis heute entwickelten Algorithmen zur Lösung des Rucksackproblems haben eine exponentielle Komplexität. Es ist kein Algorithmus bekannt, der das Rucksackproblem mit polynomialem Zeitaufwand löst. Vieles spricht dafür, dass das Rucksackproblem nicht zur Klasse der Probleme mit polynomialer Komplexität gehört. Eine endgültige Klärung dieser Komplexitätsfrage ist noch nicht gelungen.

Aufgaben

1. In der Abbildung oben stehen 10 Gegenstände zur Auswahl. Wie viele verschiedene Kombinationen von Gegenständen gibt es? Zu den Kombinationen sollen auch solche Fälle wie "keinen Gegenstand einpacken" und "alle Gegenstände einpacken" zählen.
2. Angenommen, es wären 11 bzw. 12 Gegenstände zur Auswahl, wie viele Kombinationen von Gegenständen gibt es dann?
3. Bei diesen angegebenen Algorithmus wird auf dieser Seite von einem "naiven" Algorithmus geschrieben - warum? (anders formuliert: was ist dabei nicht gut?)
4. Um das Problem besser in den Griff zu bekommen, wird "dynamische Programmierung" angegeben. Was versteht man darunter?
5. Das Rucksack-Problem gehört in die Kategorie "NP-schwer". Was versteht man darunter?

Weblinks

1. Rucksackproblem
2. Ein Rucksack voller Geschenke + Das Rucksackproblem
3. Kombinationen ausprobieren + Ein Algorithmus zum Lösungsverfahren + Eine Implementierung zum Algorithmus
4. Komplexität des Algorithmus + Komplexität des Problems
5. Rucksackproblem (Tino Hempel)
6. Rucksackproblem (Wikipedia)
7. Rucksackproblem (Robert Sedgewick)
8. Verfahren zur Lösung von 0-1-RucksackProblemen - Theorie und Implementierung
9. Rucksackproblem als dynamische Programmierung
10. Das Rucksack-Problem (Folien - Uni Bremen)

zurück